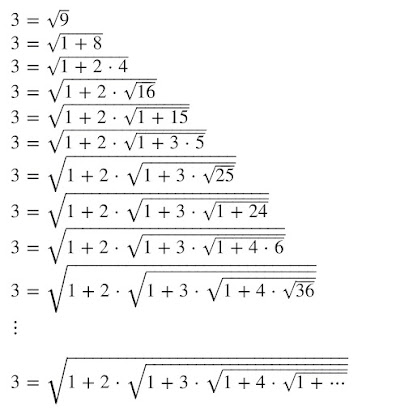Reassurance

Source: David L. Goodstein: States of Matter, Dover Publications 2002.

A nested radical

The following nested radical was proposed by Srinivasa Ramanujan in [1].

A quick proof of this remarkable identity is the following:

As noted by Ramanujan himself [2], it can be generalized to a vast class of nested radicals, see [3].

References.
[1] S. Ramanujan, J. Indian Math. Soc. 3 (1911), p. 90
[2] S. Ramanujan, J. Indian Math. Soc. 4 (1912), p. 226
[3] K. Srinivasa Rao, G. Vanden Berghe: On an entry of Ramanujan in his Notebooks: a nested roots expansion, Journal of Computational and Applied Mathematics Volume 173, Issue 2, 15 (2005) 371-378, https://doi.org/10.1016/j.cam.2004.04.009

Images Credits: Cliff Pickover (@pickover) and Kai (@UnderAntares) on Twitter

Funzioni continue su sfere, I

Consideriamo la sfera unitaria $S^n \subset \mathbb{R}^{n+1}$ e una funzione continua $f \colon S^n \longrightarrow \mathbb{R}$. Allora esiste almeno una coppia di punti antipodali che assumono lo stesso valore; in altre parole, esiste almeno un punto $x \in S^n$ tale che $f(x) = f(-x)$.

Una semplice dimostrazione di questo fatto passa attraverso la funzione ausiliaria

$$g(x) = \frac{f(x)-f(-x)}{|f(x)-f(-x)|}, $$ che assume valori in $\{-1, \, 1\}$. Se fosse $f(x) \neq f(-x)$ per ogni $x \in S^n$, la funzione $g$ sarebbe definita con continuità su tutta la sfera e si avrebbe $$g(-x)= \frac{f(-x)-f(x)}{|f(-x)-f(x)|}= -g(x).$$ Dunque si otterrebbe una funzione continua e suriettiva $g \colon S^n \longrightarrow \{-1, \, 1\}$, una contraddizione in quanto $S^n$ è uno spazio topologico connesso.

Vale in realtà un risultato più forte, noto come Teorema di Borsuk-Ulam [1, 2]: data ogni funzione continua $f \colon S^n \longrightarrow \mathbb{R}^n$, esiste almeno un punto $x \in S^n$ tale che $f(x) = f(-x)$. Il caso trattato sopra si ottiene da questo componendo $f \colon S^n \longrightarrow \mathbb{R}$ con un'inclusione continua $\mathbb{R} \longrightarrow \mathbb{R}^n$.

Se si provasse a dimostrare Borsuk-Ulam per assurdo adattando l'argomento visto sopra, si otterrebbe una funzione continua e dispari $g \colon S^n ⟶ S^{n-1}$. Tale funzione in effetti non può esistere, ma la dimostrazione di questo fatto è più complessa e richiede alcuni concetti di Topologia Algebrica.

Una strada alternativa è quella di dimostrare Borsuk-Ulam attraverso un risultato di Combinatoria noto come Lemma di Tucker: la sitazione è analoga a quella che si ha con il Teorema del punto fisso di Brouwer, che può essere dimostrato sia per via (co)omologica che ricorrendo al Lemma di Sperner.

Il Teorema di Borsuk-Ulam sarà oggetto di uno dei prossimi post.

Riferimenti.

[1] K. Borsuk: Drei Sätze über die n-dimensionale euklidische Sphäre, Fundamenta Mathematicae 20 (1933), 177–190, doi:10.4064/fm-20-1-177-190

[2] J. Matoušek: Using the Borsuk–Ulam theorem, Springer Verlag 2003.

I am not dressed properly

Il matematico ungherese László Lovász aveva accettato di rilasciare un'intervista alla Eötvös Loránd University su alcuni aspetti del suo lavoro.

Durante il colloquio, la Segretaria Generale dell'Accademia Norvegese delle Scienze gli comunica inaspettatamente che gli è stato assegnato il premio Abel 2021, insieme ad Avi Wigderson, per i suoi profondi contributi alla Combinatoria e all'Informatica Teorica.

Stupito, Lovász riesce solo a dire: "Thank you, I am not dressed properly for this kind of situation."

Fonte: The Abel Prize's YouTube Channel.

Il teorema del punto fisso di Brouwer

Teorema. Sia $\mathbb{D}^{n+1}$ la palla chiusa di $\mathbb{R}^{n+1}$. Allora ogni funzione continua $f \colon  \mathbb{D}^{n+1} \longrightarrow \mathbb{D}^{n+1}$ ammette almeno un punto fisso, ossia esiste almeno un punto $x \in \mathbb{D}^{n+1}$ tale che $f(x)=x.$

Questo celebre ed importante risultato venne dimostrato per la prima volta (indipendentemente) da L. E. J. Brouwer e da J. Hadamard, vedi [1] e [2]. In generale, il punto fisso non è unico: si pensi ad una riflessione rispetto ad un iperpiano di simmetria della palla, che ha infiniti punti fissi. Vogliamo qui riprodurre la classica, breve dimostrazione del Teorema del punto fisso di Brouwer che fa uso di tecniche standard di Topologia Algebrica e che illustra la potenza degli argomenti di tipo funtoriale.

Supponiamo per assurdo che $f$ non ammetta punti fissi. Allora possiamo definire una funzione $r \colon  \mathbb{D}^{n+1} \longrightarrow S^n$, associando ad ogni punto $x \in \mathbb{D}^{n+1}$  l'intersezione col bordo della palla della semiretta uscente da $f(x)$ e contenente $x$.

La funzione $r$ è continua, dato che $f$ lo è, e per costruzione fissa tutti i punti del bordo. Si tratta dunque di una retrazione di $\mathbb{D}^{n+1}$ su $S^n$, ossia di un'applicazione continua $\mathbb{D}^{n+1} \longrightarrow S^n$ tale che la composizione con l'inclusione $$S^n \hookrightarrow \mathbb{D}^{n+1} \longrightarrow S^n$$ è l'identità di $S^n$. Ma una tale retrazione non può esistere. Infatti, passando in coomologia singolare e applicando il funtore $H^n(\quad, \, \mathbb{Z})$, si avrebbe che l'identità $$\mathbb{Z} \simeq H^n(S^n,  \, \mathbb{Z}) \longrightarrow H^n(S^n,  \, \mathbb{Z}) \simeq \mathbb{ℤ}$$ dovrebbe fattorizzare attraverso il gruppo $H^n(\mathbb{D}^{n+1}, \, \mathbb{Z})$. Siccome la palla è contraibile, tale gruppo è banale e quindi l'identità fattorizzerebbe attraverso un'applicazione costante, contraddizione.

Riferimenti.

[1] L. E. J. Brouwer: Über Abbildungen von Mannigfaltigkeiten, Mathematische Annalen 71: 97–115 (1911), doi:10.1007/BF01456931.

[2] J. Hadamard: Note sur quelques applications de l’indice de Kronecker in Jules Tannery: Introduction à la théorie des fonctions d’une variable (Volume 2), 2nd edition, A. Hermann & Fils, Paris 1910, pp. 437–477.

Old times

Before functoriality, people lived in caves.

- Attributed to Brian Conrad -

L'irrazionalità di $\cos 1$

Da un tweet di @fermatslibrary, una veloce dimostrazione che $\cos 1$ è irrazionale (gli angoli sono misurati in gradi).

Dalle usuali formule di addizione segue $$\cos(n+1) + \cos(n-1) = 2 \cos 1 \, \cos n$$ e quindi $\cos 2=2 \cos^2 1 - 1.$ Per induzione otteniamo che $\cos n$ è una espressione razionale in $\cos 1$ per ogni $n \in \mathbb{N}$ e, quindi, $\cos 1$ non può essere razionale in quanto $\cos 30=\sqrt{3}/2$ non lo è.

Rigor

Besides, it is an error to believe that rigor in the proof is the enemy of simplicity. [...] The very effort for rigor forces us to find out simpler methods of proof.

Source: 

David Hilbert: Mathematical Problems, Lecture delivered before the International Congress of Mathematician at Paris in 1900. Bull. Amer. Math. Soc. Vol.8, No. 10 (1902), p. 441.